Triângulos

• Um triângulo equilátero possui todos os lados congruentes ou seja iguais. Um triângulo equilátero é também equiângulo: todos os seus ângulos internos são congruentes (medem 60°), sendo, portanto, classificado como um polígono regular.
• Um triângulo isósceles possui pelo menos dois lados de mesma medida e dois ângulos congruentes. O triângulo equilátero é, conseqüentemente, um caso especial de um triângulo isósceles, que apresenta não somente dois, mas todos os três lados iguais, assim como os ângulos, que medem todos 60º. Num triângulo isósceles, o ângulo formado pelos lados congruentes é chamado ângulo do vértice. Os demais ângulos denominam-se ângulos da base e são congruentes.
• Em um triângulo escaleno, as medidas dos três lados são diferentes. Os ângulos internos de um triângulo escaleno também possuem medidas diferentes.

Denomina-se base o lado sobre qual se apóia o triângulo. No triângulo isósceles, considera-se base o lado de medida diferente.
Todos esses triângulos são os mesmos encontrados num plano de duas dimensões, porem em grandes extensões, como na superfície do planeta por exemplo, os ângulos para continuarem os mesmos é necessário que o comprimento dos lados sejam deformados ou seja ampliados em igual proporção ao perímetro da esfera.

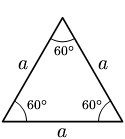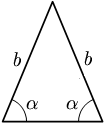Equilátero	Isósceles	Escaleno

Um triângulo também pode ser classificado de acordo com seus ângulos internos:

• Um triângulo retângulo possui um ângulo reto. Num triângulo retângulo, denomina-se hipotenusa o lado oposto ao ângulo reto. Os demais lados chamam-se catetos. Os catetos de um triângulo retângulo são complementares.
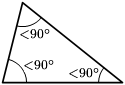
• Um triângulo obtusângulo possui um ângulo obtuso e dois ângulos agudos.
• Em um triângulo acutângulo, os três ângulos são agudos(formando 180°).

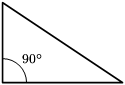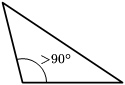Retângulo	Obtusângulo	Acutângulo

[editar] Condição de existência de um triângulo

Para que se possa construir um triângulo é necessário que a medida de qualquer um dos lados seja menor que a soma das medidas dos outros dois e maior que o valor absoluto da diferença entre essas medidas.
| b − c | < a < b + c
o triângulo é um aspecto lítico da fisica, aritmética e geometria.

[editar] Fatos básicos

Fatos elementares sobre triângulos foram apresentados por Euclides nos livros 1-4 de sua obra Elementos aproximadamente em 300 a.C..
Um triângulo é um polígono.
Dois triângulos são ditos semelhantes se um pode ser obtido pela expansão uniforme do outro. Este é o caso se, e somente se, seus ângulos correspondentes são iguais, e isso ocorre, por exemplo, quando dois triângulos compartilham um ângulo e os lados opostos a esse ângulo são paralelos entre si. O fato crucial sobre triângulos similares é que os comprimentos de seus lados são proporcionais. Isto é, se o maior lado de um triângulo é duas vezes o maior lado do triângulo similar, diz-se, então, que o menor lado será também duas vezes maior que o menor lado do outro triângulo, e o comprimento do lado médio será duas vezes o valor do lado correspondente do outro triângulo. Assim, a razão do maior lado e o menor lado do primeiro triângulo será a mesma razão do maior lado e o menor lado do outro triângulo.
Usando-se triângulos retângulos e o conceito de similaridade, as funções trigonométricas de seno e cosseno podem ser definidas. Essas são funções de um ângulo que são investigadas na trigonometria.
Nos casos a seguir, será usado um triângulo com vértices A, B e C, ângulos α, β e γ e lados a, b e c. O lado a é oposto ao vértice A e ao ângulo α, o lado b é oposto ao vértice B e ao ângulo β e o lado c é oposto ao vértice C e ao ângulo γ.
Na geometria Euclidiana, de acordo com o Teorema angular de Tales, a 32ª proposição de Euclides afirma que a soma dos ângulos internos de qualquer triângulo é igual a dois ângulos retos (180° ou π radianos). Isso permite a determinação da medida do terceiro ângulo, desde que sejam conhecidas as medidas dos outros dois ângulos.
Ex:

Os ângulos A e A' são iguais (duas paralelas cortadas por uma transversal). Os ângulos B e B' são iguais por serem alternos internos. Os ângulos C e C' são iguais por serem opostos pelo vértice. Assim vê-se que a soma dos ângulos internos do triângulo é 180º.

Existe um Corolário desse Teorema, que afirma que a medida de um ângulo externo de um triângulo é igual à soma das medidas dos ângulos internos não-adjacentes.
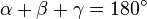
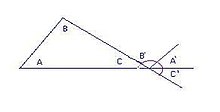
Ex: Sendo e a medida do ângulo externo do triângulo que tem como vértice o vértice C, pode-se afirmar que: e = α + β

Teorema de Pitágoras.

Um teorema central é o Teorema de Pitágoras, que afirma que em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos. Se o vértice C do exemplo dado for um ângulo reto, pode-se escrever isso da seguinte maneira:
c² = a² + b²
Isso significa que, conhecendo as medidas de dois lados de um triângulo retângulo, pode-se calcular a medida do terceiro lado — propriedade única dos triângulos retângulos.
O Teorema de Pitágoras pode ser generalizado pela lei dos cossenos:

Essa lei é válida para todos os triângulos, mesmo se γ não for um ângulo reto e pode ser usada para determinar o tamanho de lados e ângulos de um triângulo, desde que a medida de três ou dois lados e de um ângulo interno sejam conhecidas.
A lei dos senos diz: , onde d é o diâmetro da circunferência circunscrita ao triângulo (uma circunferência que passa pelos três vértices do triângulo). A lei dos senos pode ser usada para computar a medidas dos lados de um triângulo, desde que a medida de dois ângulos e de um lado sejam conhecidas.
Existem dois triângulos retângulos especiais que aparecem frequentemente em geometria. O chamado "triângulo 45º-45º-90º" possui ângulos com essas medidas e a proporção de seus lados é: 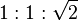. O "triângulo 30º-60º-90º" possui ângulos com essas medidas e a proporção de seus lados é: .

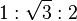[editar] Área

Produto Base Altura
A área de um triângulo é a metade do produto da medida da sua altura pela medida da sua base. Assim, a área do triângulo pode ser calculada pela fórmula:
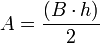, onde h é a altura do triângulo, b a medida da base.
Triângulos equiláteros
Se o triângulo for equilátero de lado l, sua área A pode ser obtida com:
.
Ou então usando sua altura h e a fórmula da base vezes a altura. A altura h de um triângulo equilátero é:
.
Vale notar que essas duas fórmulas para os triângulos equiláteros são obtidas usando as funções seno ou cosseno e usando a altura do triângulo, que o divide ao meio em dois triângulos retângulos iguais.
Semiperímetro

Outra maneira de calcular sua área é através do Teorema de Herão (ou Heron), também conhecido como fórmula do semi-perímetro:
,
onde
é o semi-perímetro.
Lados
Também podemos calcular a área a partir dos lados do triângulo. Sendo a e b dois lados quaisquer de um triângulo, e α o ângulo entre eles, temos que a área é:
.